Introduction
Since the first lattice-based cryptography results in [Ajtai96], lattices have become a central building block in quantum-resistant cryptosystems. Based on solving systems of linear equations, lattice-based cryptography adds size constraints or error terms to linear systems of equations, turning them into quantum-computer resistant one-way or trapdoor functions. Since the first theoretical cryptosystems of the 90’s and early 2000s, lattice-based cryptography has been a very active area of research, resulting in ever-more practical signature and encryption schemes, and yielding many advances in areas such as fully-homomorphic encryption.
This two-part blog series aims to provide some intuition on the main building blocks that are used in the construction of the two lattice-based signature schemes selected for standardization by the National Institute of Standards and Technology (NIST), Dilithium and Falcon, and showcases the techniques used in many other lattice-based constructions. This first part will describe a construction using lattice-based trapdoor functions and the hash-and-sign paradigm, which is at the core of the signature scheme Falcon. The second part will describe a construction based on the Fiat-Shamir paradigm, which is at the core of the signature scheme Dilithium.
Table of Contents
Lattice Background
Before diving into signature constructions, we must first introduce a few concepts about lattices and lattice-based hard problems.
At a high level, lattices can simply be thought of as the restriction of vector spaces to a discrete subgroup. In particular, a lattice is defined as the set of integer linear combinations of a set of basis vectors 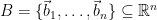 . For simplicity, we often restrict ourselves to integer lattices, i.e. lattices with basis vectors chosen from
. For simplicity, we often restrict ourselves to integer lattices, i.e. lattices with basis vectors chosen from 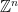 .
.
Similarly to vector spaces, a lattice can be defined by an infinite number of equivalent bases. Two bases 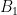 and
and 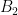 define the same lattice if every point in the lattice generated by
define the same lattice if every point in the lattice generated by 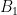 can also be generated as an integer linear combination of the basis
can also be generated as an integer linear combination of the basis 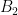 , and vice versa1. For example, the two-dimensional lattice
, and vice versa1. For example, the two-dimensional lattice 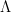 generated by
generated by 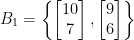 can instead be generated from the basis
can instead be generated from the basis 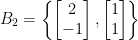 , as depicted below.
, as depicted below.
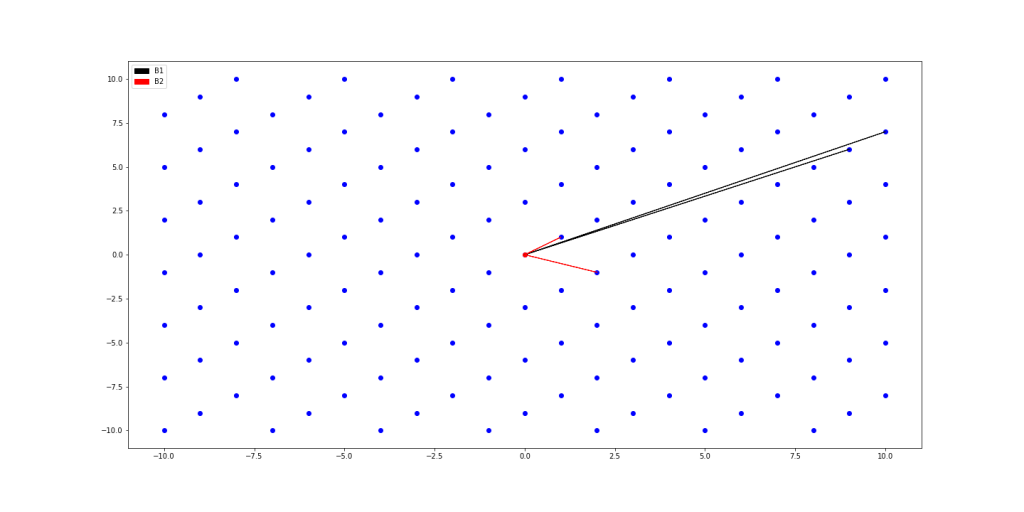
Note that, unlike standard vector spaces, not all linearly independent sets of  lattice vectors form a basis for a given lattice. For example, the set
lattice vectors form a basis for a given lattice. For example, the set 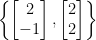 is not a basis for the lattice
is not a basis for the lattice 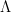 , as there is no integer linear combination of the basis vectors that generates the vector
, as there is no integer linear combination of the basis vectors that generates the vector 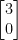 , while we can write
, while we can write 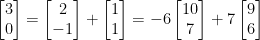 .
.
Each basis 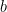 naturally corresponds to a space known as the fundamental parallelepiped, defined as the set
naturally corresponds to a space known as the fundamental parallelepiped, defined as the set 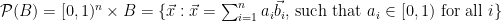 . Graphically, this corresponds to the
. Graphically, this corresponds to the 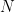 -dimensional parallelepiped with sides equal to the basis vectors, and defines a natural tiling for the space underlying the lattice. While a fundamental parallelepiped is closely tied to the basis that generated it, and is thus not unique for a given lattice, the volume enclosed by a fundamental parallelepiped is identical regardless of which lattice basis is chosen, and is thus a lattice invariant.
-dimensional parallelepiped with sides equal to the basis vectors, and defines a natural tiling for the space underlying the lattice. While a fundamental parallelepiped is closely tied to the basis that generated it, and is thus not unique for a given lattice, the volume enclosed by a fundamental parallelepiped is identical regardless of which lattice basis is chosen, and is thus a lattice invariant.
Some of the (conjectured) hardest computational problems over lattices are finding short vectors in an arbitrary lattice, known as the Shortest Vector Problem (SVP), and finding the lattice point closest to a target 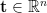 , known as the Closest Vector Problem (CVP). We can also define approximation versions of each, SVP
, known as the Closest Vector Problem (CVP). We can also define approximation versions of each, SVP and CVP
and CVP , which ask to find a short vector of length up to a multiplicative approximation factor
, which ask to find a short vector of length up to a multiplicative approximation factor 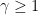 of the length of the shortest vector, or close vector of distance up to a multiplicative approximation factor
of the length of the shortest vector, or close vector of distance up to a multiplicative approximation factor 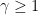 of the distance of the closest vector from the target, respectively.
of the distance of the closest vector from the target, respectively.
The effort required to solve each of the problems increases with the dimension 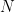 , and as the approximation factor gets closer to
, and as the approximation factor gets closer to 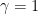 . In particular, while there exist efficient algorithms for solving the SVP and the CVP for low dimension such as
. In particular, while there exist efficient algorithms for solving the SVP and the CVP for low dimension such as 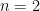 or for exponential approximation factors
or for exponential approximation factors 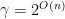 , the problems are NP-hard for large dimensions
, the problems are NP-hard for large dimensions 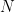 and low approximation factors. Modern lattice cryptography chooses underlying problems with dimension around
and low approximation factors. Modern lattice cryptography chooses underlying problems with dimension around 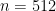 and approximation factors around
and approximation factors around 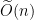 , although the exact choices of parameters for the constructions we present will be omitted from this blog post for simplicity.
, although the exact choices of parameters for the constructions we present will be omitted from this blog post for simplicity.
Note:
Lattices can be defined over a number of various algebraic structures. They can be defined over the real numbers, such as the examples above, but are often defined over 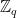 , rings or modules, as those result in more efficient implementations due to the presence of additional structure within the lattice. Whether this extra structure affects the hardness of lattice problems is an open question, but to the best knowledge of the community it is not exploitable in the cryptographic settings.
, rings or modules, as those result in more efficient implementations due to the presence of additional structure within the lattice. Whether this extra structure affects the hardness of lattice problems is an open question, but to the best knowledge of the community it is not exploitable in the cryptographic settings.
In both of our examples in this blog post series, we will use one particular family of lattices known as the 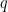 -ary lattices, which are defined as follows, for some
-ary lattices, which are defined as follows, for some 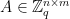 :
: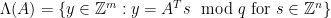
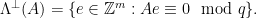
These lattices are mutually orthogonal, as each consists of exactly the vectors orthogonal to all the vectors in the other one. This property is particularly useful for checking membership of a vector in a lattice: if 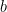 is a basis for
is a basis for 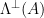 , then checking if
, then checking if 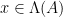 can be done by checking whether
can be done by checking whether 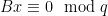 , and similarly checking whether
, and similarly checking whether 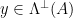 can be done by the check
can be done by the check 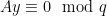 .
.
The more practical constructions, including the NIST submissions Falcon and Dilithium, often choose orthogonal lattices over rings or modules as the basis of their constructions. For the rest of this blog post, we will generally not go into the details of the specific rings or modules used, for simplicity, but we will mention what lattice constructions are used in practice.
Constructing Signatures Using Hash-and-Sign and CVP
The first construction for lattice-based signature schemes uses the hash-and-sign paradigm, and relies on the hardness of the CVP problem. The hash-and-sign paradigm was first introduced by Bellare and Rogaway [BR96] to construct the RSA Full Domain Hash (FDH) signature scheme, and relies on a secret trapdoor function for the construction of signatures.
The basic idea is simple: Suppose we have a trapdoor function 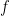 such that
such that 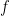 is efficiently computable, but very hard to invert (i.e.
is efficiently computable, but very hard to invert (i.e. 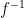 is difficult to compute) without additional information. To sign a message
is difficult to compute) without additional information. To sign a message 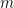 , we can hash
, we can hash 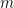 to a point
to a point 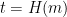 in the range of the function
in the range of the function 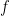 , and use the secret
, and use the secret 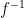 to compute the signature
to compute the signature 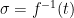 . To verify a signature
. To verify a signature 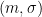 , simply compute
, simply compute 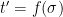 and check whether
and check whether 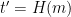 .
.
In particular, choosing the trapdoor permutation function 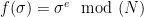 and inverse
and inverse 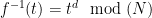 in the above set-up recovers the RSA FDH scheme.
in the above set-up recovers the RSA FDH scheme.
The Hard Problem
To see how to construct a hash-and-sign trapdoor function using lattice-based primitives, consider the closest vector problem. The CVP is a hard problem to solve2 for a random lattice, but it is easy to verify a given solution: given a target
is a hard problem to solve2 for a random lattice, but it is easy to verify a given solution: given a target 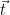 and a candidate solution (i.e. candidate close lattice vector)
and a candidate solution (i.e. candidate close lattice vector) 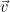 , it is easy to check that
, it is easy to check that 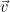 is in a given lattice, by checking whether it can be written as an integer linear combination of the basis vectors, and whether
is in a given lattice, by checking whether it can be written as an integer linear combination of the basis vectors, and whether 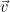 is within the specified distance of the target by computing
is within the specified distance of the target by computing 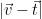 .
.
However, in order to use the CVP to construct a trapdoor function, we need to find a way to tie the hardness of the CVP
to construct a trapdoor function, we need to find a way to tie the hardness of the CVP to some secret data, i.e. ensure that a close vector can easily be found using the secret data, but is very hard to find without it. The central idea used here is the observation that not all lattice bases are created equal, and that some bases allow us to solve hard lattice problems such as CVP
to some secret data, i.e. ensure that a close vector can easily be found using the secret data, but is very hard to find without it. The central idea used here is the observation that not all lattice bases are created equal, and that some bases allow us to solve hard lattice problems such as CVP more efficiently than others. Crucially, while any basis can be used to verify the correctness of a CVP
more efficiently than others. Crucially, while any basis can be used to verify the correctness of a CVP solution (as they all define the same lattice, and thus can all be used to check a candidate solution’s membership in the lattice), the quality of a CVP
solution (as they all define the same lattice, and thus can all be used to check a candidate solution’s membership in the lattice), the quality of a CVP solution one can find (i.e. the distance from the target, measured by the size of the
solution one can find (i.e. the distance from the target, measured by the size of the 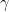 factor) depends on the basis one started off with. To see why, consider the following intuitive algorithm for solving CVP
factor) depends on the basis one started off with. To see why, consider the following intuitive algorithm for solving CVP , called Babai’s round-off algorithm:
, called Babai’s round-off algorithm:
Given a basis 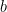 and a target point
and a target point 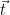 , one can use the known basis to round to a nearby lattice point as follows: write the target point as a linear combination of the basis vectors,
, one can use the known basis to round to a nearby lattice point as follows: write the target point as a linear combination of the basis vectors, 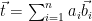 . Then, round each coefficient
. Then, round each coefficient 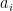 to the nearest integer, to obtain
to the nearest integer, to obtain 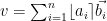 . These operations can be expressed as
. These operations can be expressed as 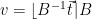 . Since any integer linear combination of lattice vectors is a lattice vector, the result
. Since any integer linear combination of lattice vectors is a lattice vector, the result 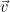 is a lattice vector near
is a lattice vector near 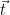 , which corresponds to the nearest corner of the fundamental parallelepiped translate containing
, which corresponds to the nearest corner of the fundamental parallelepiped translate containing 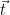 .
.
Intuitively, shorter (and more orthogonal) bases lead to more reliable results from Babai’s rounding algorithm. This can be formalized by observing that the maximum distance from the target contributed at step 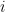 is given by
is given by 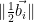 (since the solution found will be at one of the corners of the containing fundamental parallelepiped), and hence by the triangle inequality the distance
(since the solution found will be at one of the corners of the containing fundamental parallelepiped), and hence by the triangle inequality the distance 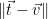 is bounded by
is bounded by 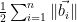 .
.
This can be seen in practice, by finding instances where two different bases find different solutions to the CVP , such as when the nearest lattice point is not in the fundamental parallelepiped containing the target point. Two examples of differing solutions can be seen in the following figure:
, such as when the nearest lattice point is not in the fundamental parallelepiped containing the target point. Two examples of differing solutions can be seen in the following figure:
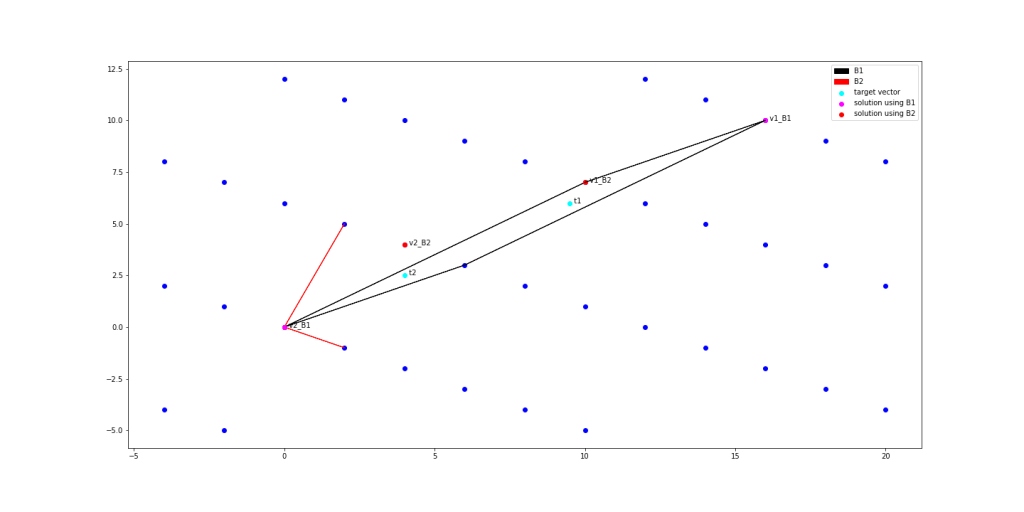
Thus, to instantiate our trapdoor algorithm, one needs to find a good basis, that allows us to solve CVP to within a certain bound, as well as a bad basis, that does not allow solving CVP
to within a certain bound, as well as a bad basis, that does not allow solving CVP without significant computational costs, but still allows one to verify solutions.
without significant computational costs, but still allows one to verify solutions.
Note:
One method for generating this pair of bases is to choose a “good” basis, and apply a transformation to it to obtain a “bad” basis. A common choice of “bad” basis is the Hermite Normal Form (HNF) of the lattice, as it is in a sense the worst possible basis: the same HNF can be generated from any basis of a given lattice, and thus the HNF reveals no information about the basis it was generated from.
A First Attempt
A signature scheme based on this idea was first proposed in 1997 by Goldreich Goldwasser and Halevi, known as the GGH signature scheme [GGH]. At its core, the GGH signature scheme chooses a “good” basis for its secret key, and computes a matching “bad” public basis to use for verifying.
- To sign a message
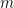 using GGH, one maps the message to a random target point
using GGH, one maps the message to a random target point 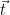 in the underlying space, and uses the secret (“good”) basis to find a solution
in the underlying space, and uses the secret (“good”) basis to find a solution 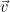 to the CVP
to the CVP with target
with target 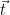 using Babai’s rounding algorithm. The signature is then
using Babai’s rounding algorithm. The signature is then 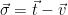 .
. - To verify the signature
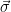 , one recomputes
, one recomputes 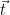 from the message
from the message 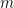 , checks that
, checks that 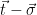 is a lattice vector using the public basis, and that
is a lattice vector using the public basis, and that 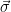 is sufficiently short (by checking that
is sufficiently short (by checking that 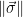 is below some publicly known bound, chosen as part of the signature scheme parameters).
is below some publicly known bound, chosen as part of the signature scheme parameters).
(One could equivalently define the signature as the value 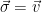 , and check that
, and check that 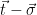 is short and that
is short and that 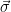 is a lattice vector during verification).
is a lattice vector during verification).
The GGH signature scheme was chosen as a foundation for the original NTRUSign signature scheme, by instantiating it with a lattice defined over a special class of rings (the NTRU lattice) which allows for a much more compact representation of the underlying lattice, leading to better efficiency and smaller keys.
Breaking the GGH/NTRUSign Signature Scheme
Unfortunately, the GGH signature construction leaks information about the secret basis with every new signature. Indeed, if a secret basis 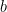 was used to generate GGH signatures (where
was used to generate GGH signatures (where 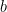 is represented as a matrix), each signature can be mapped to a point in the fundamental parallelepiped defined by the (secret) basis
is represented as a matrix), each signature can be mapped to a point in the fundamental parallelepiped defined by the (secret) basis 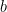 , and thus leak information about this secret basis.
, and thus leak information about this secret basis.
Indeed, if 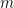 is mapped to the target point
is mapped to the target point 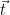 , the nearby lattice point found is
, the nearby lattice point found is 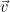 and the corresponding signature is
and the corresponding signature is 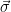 , then we can rewrite
, then we can rewrite 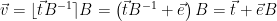 , for
, for ![\vec{e} \in [-1/2,1/2]^n](/media/f13mykij/_-vec-e-in-1-2-1-2-n.png) by choice of
by choice of 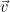 and the definition of Babai’s rounding algorithm, and hence
and the definition of Babai’s rounding algorithm, and hence
![\vec{\sigma} = \vec{t} - \vec{v} = \vec{e} \in [-1/2,1/2]^nB = \{xB: x \in [-1/2,1/2]^n \}](/media/lltd0ay1/_-vec-sigma-vec-t-vec-v-vec-e-in-1-2-1-2-nb-xb-x-in-1-2-1-2-n.png) .
.
This can be seen graphically in the following figure, where we see that each new message signature pair corresponds to a point in the fundamental parallelepiped defined by the basis used to generate it. The following figure plots the 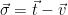 values obtained from signatures generated using the two bases defined above:
values obtained from signatures generated using the two bases defined above:
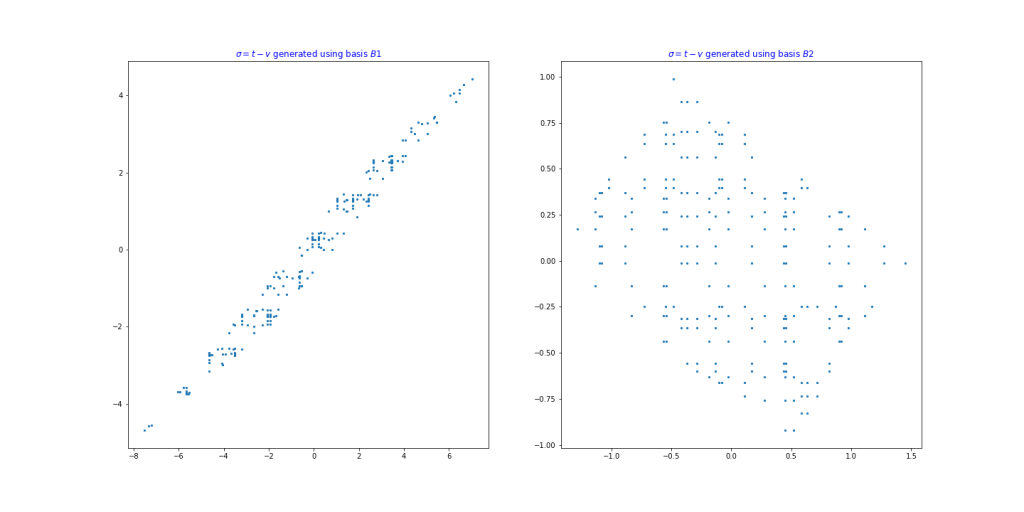
Nguyen and Regev [NR06] showed that this method can be used to recover the secret basis with a few hundred message signature pairs, by using standard optimization techniques to recover the basis from these points in the fundamental parallelepiped.
Note:
The Nearest Planes Algorithm is an algorithm very similar to Babai’s round-off algorithm for solving CVP that rounds based on the Gram-Schmidt vectors of the basis instead of the basis vectors themselves, and has very similar asymptotic hardness guarantees. While the GGH construction chose to use Babai’s rounding algorithm to solve CVP
that rounds based on the Gram-Schmidt vectors of the basis instead of the basis vectors themselves, and has very similar asymptotic hardness guarantees. While the GGH construction chose to use Babai’s rounding algorithm to solve CVP , the Nearest Planes Algorithm can equivalently be used instead.
, the Nearest Planes Algorithm can equivalently be used instead.
A Secure Signature Scheme Based on CVP – GPV08 Signatures
Despite the flaws in the GGH construction, the high-level idea of using a short basis as a trapdoor can still be made to work. In 2008, Gentry, Peikert and Vaikuntanathan [GPV08] showed how this lattice trapdoor framework can be adapted to create provably secure signatures.
The fundamental idea is simple: given a set of signatures 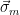 , we wish the distribution of these signatures to leak no information about the trapdoor function used to generate them. In particular, if the distribution of the signatures (over some fixed domain) is independent of the secret values used, no information can be leaked from the signatures using this method. Note that this was not the case with the GGH signature scheme, as the domain of the distribution was closely related to the geometry of the secret values.
, we wish the distribution of these signatures to leak no information about the trapdoor function used to generate them. In particular, if the distribution of the signatures (over some fixed domain) is independent of the secret values used, no information can be leaked from the signatures using this method. Note that this was not the case with the GGH signature scheme, as the domain of the distribution was closely related to the geometry of the secret values.
Getting this to work in the lattice setting requires a slight generalization of the usual definition of trapdoor functions. A trapdoor permutation 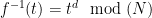 , used for instance in RSA FDH, defines a unique inverse for each element of the range. Choosing elements of the range of
, used for instance in RSA FDH, defines a unique inverse for each element of the range. Choosing elements of the range of 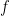 uniformly (which could be done for instance by hashing a message to a random element of the range) thus results in a uniform distribution of signatures over to the domain of
uniformly (which could be done for instance by hashing a message to a random element of the range) thus results in a uniform distribution of signatures over to the domain of 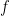 (or range of
(or range of 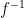 ) and prevents the leak of any information about the secret integer
) and prevents the leak of any information about the secret integer 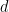 from the distribution of the signatures.
from the distribution of the signatures.
However, if we want to base our lattice trapdoors on the hardness of CVP , there are multiple lattice points within a fixed, relatively short distance from the target, and hence each element of the range has multiple possible preimages. One must thus ensure that the distribution over these preimages obtained during the signing process leaks no information about the inversion function. That is, we want to define a trapdoor function
, there are multiple lattice points within a fixed, relatively short distance from the target, and hence each element of the range has multiple possible preimages. One must thus ensure that the distribution over these preimages obtained during the signing process leaks no information about the inversion function. That is, we want to define a trapdoor function 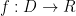 that can only be inverted efficiently using some secret data, and such that the domain
that can only be inverted efficiently using some secret data, and such that the domain 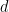 and distribution
and distribution 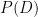 over the domain obtained by choosing a uniformly random element of the range
over the domain obtained by choosing a uniformly random element of the range  (e.g. by hashing a message
(e.g. by hashing a message 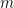 to an element of
to an element of  ) and inverting the trapdoor function (computing
) and inverting the trapdoor function (computing 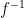 ) are independent of the secret data used to compute
) are independent of the secret data used to compute 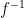 .
.
Thus, the trapdoor inversion function 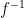 must guarantee that the output is both correct and that it follows the correct distribution, i.e. that if
must guarantee that the output is both correct and that it follows the correct distribution, i.e. that if 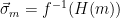 , we must have
, we must have 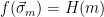 and that the distribution of all
and that the distribution of all 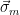 values is exactly
values is exactly 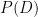 . This can be formalized using conditional distributions, i.e. by requiring that
. This can be formalized using conditional distributions, i.e. by requiring that 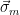 is sampled from the distribution
is sampled from the distribution 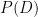 , conditioned on the fact that
, conditioned on the fact that 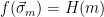 . This generalized definition was formalized in [GPV08], in which the authors called functions that satisfy these properties “Preimage Sampleable Functions”.
. This generalized definition was formalized in [GPV08], in which the authors called functions that satisfy these properties “Preimage Sampleable Functions”.
Given such a preimage sampleable (trapdoor) function 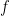 and its inverse
and its inverse 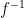 , one can define a trapdoor signature scheme in the usual way:
, one can define a trapdoor signature scheme in the usual way:
Sign(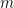 ):
1. Compute
):
1. Compute 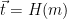 2. Output
2. Output 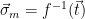 Verify(
Verify(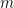 ,
, 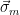 ):
1. Check that
):
1. Check that 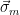 is in the domain
is in the domain 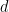 2. Check that
2. Check that 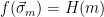 .
.Note that this definition avoids the problems with the GGH signature scheme. Indeed, if the domain 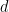 and the distribution of signatures
and the distribution of signatures 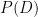 over the domain are independent of the secret values, signatures chosen from
over the domain are independent of the secret values, signatures chosen from 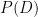 cannot leak any information about the secret values used to compute them.
cannot leak any information about the secret values used to compute them.
Preimage Samplable Trapdoor Functions from Gaussians
However, it is not immediately clear that such preimage samplable functions even exist, or how to compute them. In [GPV08], the authors showed that a Gaussian distribution can be used to define a family of preimage samplable functions, due to some nice properties of Gaussian distributions over lattices.
The basic intuition as to why Gaussian distributions are particularly useful in this case is that a Gaussian of sufficient width overlaid over a lattice can easily be mapped to a uniform distribution over the underlying space, and is thus a great candidate for instantiating a preimage samplable function. Indeed, consider sampling repeatedly from a Gaussian distribution centered at the origin, and reducing modulo the fundamental parallelepiped. As depicted in the following figure, the distribution that results from this process tends to the uniform distribution (over the fundamental parallelepiped) as the width of the Gaussian increases, and relatively small widths are sufficient to get close to a uniform distribution.
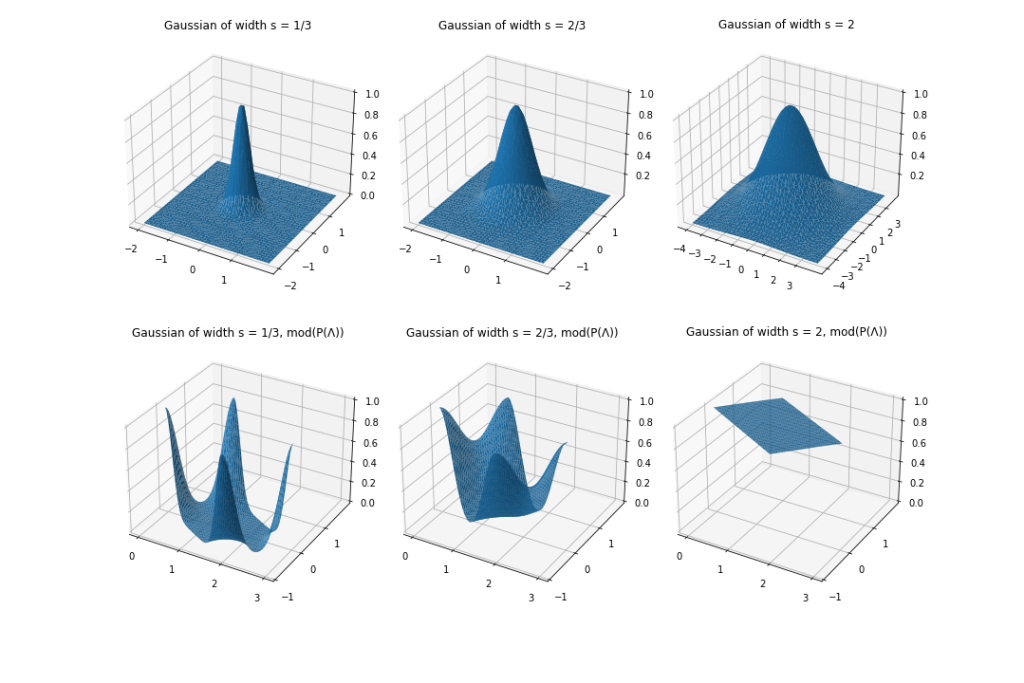
Thus, we can define the distribution 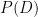 as a (truncated) Gaussian distribution
as a (truncated) Gaussian distribution 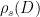 of sufficient width
of sufficient width  , with the domain
, with the domain 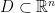 chosen to be an area that contains all but a negligible fraction of the Gaussian distribution
chosen to be an area that contains all but a negligible fraction of the Gaussian distribution 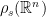 3. By the properties of the Gaussian, if
3. By the properties of the Gaussian, if 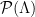 is the fundamental parallelepiped defined by the public basis for the lattice
is the fundamental parallelepiped defined by the public basis for the lattice 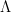 , the distribution of
, the distribution of 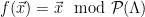 will be uniform, for
will be uniform, for 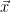 distributed as
distributed as 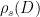 .
.
To show that 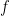 is a preimage samplable function and use it to instantiate a signature scheme, it remains to find a method to compute
is a preimage samplable function and use it to instantiate a signature scheme, it remains to find a method to compute 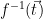 efficiently (given some secret values), i.e. define a method for sampling
efficiently (given some secret values), i.e. define a method for sampling 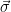 from
from 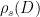 , conditioned on
, conditioned on 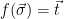 , for uniformly random targets
, for uniformly random targets 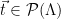 . To define this sampling method, note that all vectors
. To define this sampling method, note that all vectors 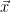 with
with 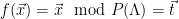 are exactly the elements of the shifted lattice
are exactly the elements of the shifted lattice 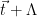 . Thus, sampling from
. Thus, sampling from 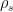 , conditioned on
, conditioned on 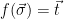 is equivalent to sampling from the distribution
is equivalent to sampling from the distribution 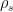 restricted to
restricted to 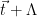 . In practice, this is done by sampling a lattice vector
. In practice, this is done by sampling a lattice vector 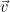 from the appropriate offset distribution
from the appropriate offset distribution 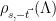 4, and outputting
4, and outputting 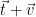 . Alternately, we can sample from
. Alternately, we can sample from 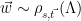 and output
and output 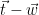 , since both the Gaussian distribution and the lattice
, since both the Gaussian distribution and the lattice 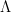 are invariant under reflection.
are invariant under reflection.
The final piece of the puzzle is to figure out how to sample from 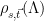 efficiently. At the core of [GPV08] was a new efficient Gaussian sampler over arbitrary lattices, which is based on the observation that one can sample from the desired Gaussian distribution over a lattice, if one knows a “good” quality basis (chosen as the secret trapdoor for this scheme)5. The resultant algorithm can be thought of as a randomized version of the nearest planes algorithm, where instead of selecting the nearest plane at each step, one selects a nearby plane, according to the (discrete) Gaussian distribution over the candidate planes. In [Pei10], Peikert showed that Babai’s round-off algorithm can be similarly randomized coordinate-by-coordinate, at the cost of an extra perturbation technique to account for the skew introduced by the fact basis vectors are generally not an orthogonal set.
efficiently. At the core of [GPV08] was a new efficient Gaussian sampler over arbitrary lattices, which is based on the observation that one can sample from the desired Gaussian distribution over a lattice, if one knows a “good” quality basis (chosen as the secret trapdoor for this scheme)5. The resultant algorithm can be thought of as a randomized version of the nearest planes algorithm, where instead of selecting the nearest plane at each step, one selects a nearby plane, according to the (discrete) Gaussian distribution over the candidate planes. In [Pei10], Peikert showed that Babai’s round-off algorithm can be similarly randomized coordinate-by-coordinate, at the cost of an extra perturbation technique to account for the skew introduced by the fact basis vectors are generally not an orthogonal set.
The output of this sampling algorithm is effectively chosen randomly from the solutions to the CVP problem, and since the resultant signatures are distributed as a Gaussian distribution that is independent from the basis, no information about the geometry of the secret basis used by the sampler is leaked. This can be formalized by noting that by definition, we have
problem, and since the resultant signatures are distributed as a Gaussian distribution that is independent from the basis, no information about the geometry of the secret basis used by the sampler is leaked. This can be formalized by noting that by definition, we have 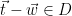 , and hence
, and hence 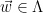 is at a distance of at most
is at a distance of at most 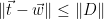 from the target
from the target 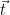 . Choosing a sufficiently small domain
. Choosing a sufficiently small domain 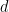 as part of the definition for the signature scheme ensures
as part of the definition for the signature scheme ensures 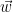 is a solution to the CVP
is a solution to the CVP problem with target
problem with target 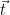 .
.
Putting this all together, we can define a CVP -based trapdoor signature scheme as follows:
-based trapdoor signature scheme as follows:
Sign(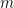 ):
1. Compute
):
1. Compute 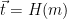 to be a uniformly random point in
to be a uniformly random point in 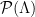 2. Compute
2. Compute 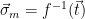 :
1. Sample
:
1. Sample 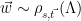 , using the secret basis for
, using the secret basis for 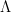 .
2. Set
.
2. Set 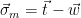 . Note that
. Note that 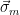 is distributed as
is distributed as 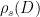 conditioned on
conditioned on 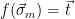 .
3. Output the signature
.
3. Output the signature 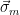 Verify(
Verify(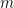 ,
, 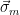 ):
1. Check that
):
1. Check that 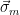 is in the domain
is in the domain 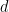 2. Recompute
2. Recompute 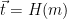 , and check that
, and check that 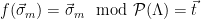 (or, equivalently, check that
(or, equivalently, check that 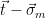 is a lattice vector, since
is a lattice vector, since 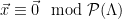 if and only if
if and only if 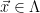 ).
).The authors of [GPV08] used this construction to define an efficient trapdoor signature scheme based on the CVP problem in lattices. Their particular instantiation is defined over a family of lattices that allows particularly efficient operations, and thus yields an efficient signature scheme. The following section goes into details about their construction, which follows the same high-level approach as was covered here. However, it is a little more technical and can be skipped if only the high-level intuition is desired.
problem in lattices. Their particular instantiation is defined over a family of lattices that allows particularly efficient operations, and thus yields an efficient signature scheme. The following section goes into details about their construction, which follows the same high-level approach as was covered here. However, it is a little more technical and can be skipped if only the high-level intuition is desired.
As a nice bonus, this lattice-based trapdoor scheme has nice provable security properties. It can be shown that the (average-case) security of this scheme can be reduced to the worst-case hardness of the well-studied hard lattice problem Shortest Independent Vector Problem (SIVP ). This is particularly nice, as the worst-case hardness of a problem is often easier to analyze than the average-case hardness (i.e. the hardness of a randomly-selected instance, such as when keys are chosen at random).
). This is particularly nice, as the worst-case hardness of a problem is often easier to analyze than the average-case hardness (i.e. the hardness of a randomly-selected instance, such as when keys are chosen at random).
The secure trapdoor construction of [GPV08] was eventually adapted in the design of the NIST candidate Falcon, which consists of [GPV08] trapdoor signatures instantiated over a special class of compact lattices called the NTRU lattices. Falcon is the smallest of the NIST PQC finalists, when comparing the total size of public key and signature, and has very fast verification. However, the implementation of Falcon has a lot of complexity – in particular, implementing the discrete Gaussian sampler securely and in constant-time is tricky, as the reference implementation uses floating point numbers for this computation.
Details of the [GPV08] Trapdoor Signature Construction
At a high-level, the [GPV08] construction relies on instantiating the above construction over a discrete domain and range, in order to allow for more efficient computations. In particular, the construction is defined over the 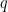 -ary lattices
-ary lattices 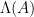 and
and 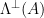 . This is done for two reasons: first, this allows for more efficient membership verification, as checking whether
. This is done for two reasons: first, this allows for more efficient membership verification, as checking whether  is in the
is in the 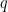 -ary lattice
-ary lattice 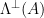 only requires checking whether
only requires checking whether 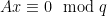 . Second, restricting ourselves to a discrete range and domain simplifies many computations, and allows us to better formalize what it means for target points to be distributed uniformly over the range, as it is easier to map the outputs of a hash function to a discrete domain than to a continuous one.
. Second, restricting ourselves to a discrete range and domain simplifies many computations, and allows us to better formalize what it means for target points to be distributed uniformly over the range, as it is easier to map the outputs of a hash function to a discrete domain than to a continuous one.
However, working with discrete 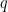 -ary lattices requires modifying the definitions and distributions to work over this new domain and range. In particular, we define the discrete Gaussian distribution over a lattice as the discrete-domain version of the Gaussian distribution which preserves these nice properties of uniformity over the chosen discrete domain in a natural way. Specifically, a smoothing discrete Gaussian distribution can be defined over a superlattice, a finer-gridded lattice
-ary lattices requires modifying the definitions and distributions to work over this new domain and range. In particular, we define the discrete Gaussian distribution over a lattice as the discrete-domain version of the Gaussian distribution which preserves these nice properties of uniformity over the chosen discrete domain in a natural way. Specifically, a smoothing discrete Gaussian distribution can be defined over a superlattice, a finer-gridded lattice 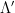 such that
such that 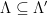 . The smoothing discrete Gaussian distribution over the superlattice,
. The smoothing discrete Gaussian distribution over the superlattice, 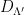 , can then be defined in such a way that it results in a uniform distribution when reduced modulo the fundamental parallelepiped. Note that the range of this mapping, i.e. the set of possible values of
, can then be defined in such a way that it results in a uniform distribution when reduced modulo the fundamental parallelepiped. Note that the range of this mapping, i.e. the set of possible values of 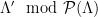 corresponds exactly to the set of cosets
corresponds exactly to the set of cosets 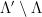 .
.
In particular, in the case of 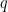 -ary lattices, we can choose
-ary lattices, we can choose 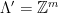 and
and 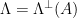 . From the definition, we get that a sufficiently wide discrete Gaussian distribution
. From the definition, we get that a sufficiently wide discrete Gaussian distribution 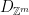 that is smoothing over the lattice
that is smoothing over the lattice 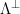 will result in a uniform distribution over the set of cosets
will result in a uniform distribution over the set of cosets 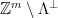 when reduced modulo the fundamental parallelepiped
when reduced modulo the fundamental parallelepiped 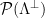 . Additionally, we can use a correspondence between the set of cosets
. Additionally, we can use a correspondence between the set of cosets 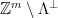 , and the set of syndromes6
, and the set of syndromes6 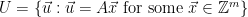 to show that if we sample
to show that if we sample 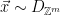 , choosing the width so that
, choosing the width so that 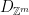 is smoothing over the lattice
is smoothing over the lattice 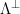 , then the distribution of
, then the distribution of 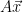 will be uniform over the set of syndromes
will be uniform over the set of syndromes 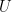 .
.
Thus, to instantiate the secure trapdoor construction of [GPV08] with 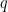 -ary lattices, messages are mapped uniformly to the set of syndromes
-ary lattices, messages are mapped uniformly to the set of syndromes 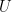 , and signatures
, and signatures 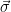 are sampled from the (smoothing) distribution
are sampled from the (smoothing) distribution 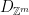 , conditioned on
, conditioned on 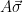 being equal to the syndrome corresponding to a particular message. Finally, we can choose parameters such that we can guarantee that for almost all choices of
being equal to the syndrome corresponding to a particular message. Finally, we can choose parameters such that we can guarantee that for almost all choices of 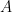 ,
, 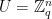 . Thus, messages only need to be mapped uniformly to
. Thus, messages only need to be mapped uniformly to 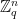 , which can be done in a straightforward manner using an appropriately defined hash function.
, which can be done in a straightforward manner using an appropriately defined hash function.
As before, sampling from the (smoothing) distribution 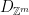 , conditioned on
, conditioned on 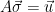 can be done by mapping the syndrome back to the corresponding coset
can be done by mapping the syndrome back to the corresponding coset 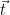 , sampling a lattice vector
, sampling a lattice vector 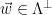 from the shifted distribution
from the shifted distribution 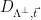 (corresponding to sampling from
(corresponding to sampling from 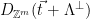 ), and outputting
), and outputting 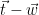 . Note that the vector
. Note that the vector 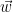 is a solution to the CVP problem with lattice
is a solution to the CVP problem with lattice 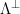 and target
and target 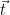 . Putting everything together, we can choose
. Putting everything together, we can choose 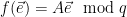 , and instantiate a trapdoor signature scheme as follows:
, and instantiate a trapdoor signature scheme as follows:
Sign(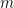 ):
1. Choose
):
1. Choose 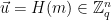 to be a uniformly random syndrome from
to be a uniformly random syndrome from 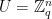 2. Compute
2. Compute 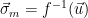 :
1. Choose
:
1. Choose 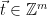 , an arbitrary preimage such that
, an arbitrary preimage such that 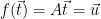 (this can be done via
standard linear algebra)
2. Sample
(this can be done via
standard linear algebra)
2. Sample 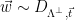 , the discrete Gaussian distribution over
, the discrete Gaussian distribution over 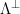 centered at
centered at 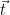 .
3. Let
.
3. Let 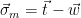 . Note that
. Note that 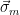 is distributed as
is distributed as 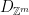 , conditioned on
, conditioned on 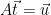 .
3. Output the signature
.
3. Output the signature 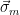 .
Verify(
.
Verify(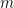 ,
, 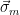 ):
1. Check whether
):
1. Check whether 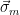 is contained in the domain
is contained in the domain 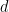 (in practice, this amounts to
checking whether
(in practice, this amounts to
checking whether 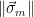 is sufficiently small).
2. Check whether
is sufficiently small).
2. Check whether 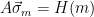 . Note that
. Note that 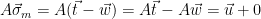 , by choice
of
, by choice
of 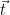 and definition of
and definition of 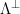 .
.Conclusion
Lattice-based [GPV08]-style trapdoor signatures are a generalization of the classical hash-and-sign signatures paradigm, that randomizes the signing process in order to account for the existence of multiple preimages and avoid leaking information about the discrete structure of the lattice. This approach allows the resultant signatures to be very short, at the cost of some implementation complexity.
While the construction may seem intimidating at first, this write-up attempts to have made this modified lattice-based construction a little more approachable. Stay tuned for the second part of this blog post series, which will describe an alternate construction for lattice-based signatures, based on the Fiat-Shamir paradigm.
Acknowledgements
I’d like to thank Paul Bottinelli, Giacomo Pope and Thomas Pornin for their valuable feedback on earlier drafts of this blog post. Any remaining errors are mine alone.
Footnotes
1: Formally, two bases 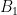 and
and 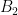 define the same lattice if and only if there is an unimodular matrix (a square, integer matrix with determinant
define the same lattice if and only if there is an unimodular matrix (a square, integer matrix with determinant 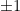 , or, equivalently, an integer matrix which is invertible over the integers)
, or, equivalently, an integer matrix which is invertible over the integers) 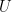 such that
such that 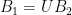 .
.
2: For an appropriately chosen instance of the CVP problem. Concretely, one usually chooses values around
problem. Concretely, one usually chooses values around 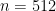 and
and 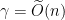 for cryptographic applications.
for cryptographic applications.
3: The exact width needed can be formalized using a quantity known as the smoothing parameter, which relates the width of a Gaussian distribution 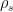 to the distance from uniform of the reduced distribution of
to the distance from uniform of the reduced distribution of 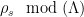 . It can be shown that relatively narrow Gaussians are sufficient to obtain a negligible distance from uniform – for instance, the lattice of integers
. It can be shown that relatively narrow Gaussians are sufficient to obtain a negligible distance from uniform – for instance, the lattice of integers 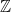 has a smoothing parameter of
has a smoothing parameter of 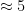 for
for 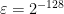 distance from uniform. The domain
distance from uniform. The domain 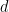 can simply be defined as all points within a certain distance from the origin, with the distance defined chosen as a small multiple of the width
can simply be defined as all points within a certain distance from the origin, with the distance defined chosen as a small multiple of the width  , since the exponential decay of the Gaussian function means almost all of the weight is given to points near the origin.
, since the exponential decay of the Gaussian function means almost all of the weight is given to points near the origin.
4: The offset distribution 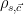 is simply a Gaussian distribution of width
is simply a Gaussian distribution of width  that is centered at the point
that is centered at the point 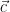 , and can be defined as
, and can be defined as 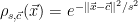
5: Any basis can be used to implement this sampler, but one can only sample from Gaussian distributions that are sufficiently wider than the longest vector in a known basis. One can thus choose a width such that the Gaussian still maps to the uniform distribution under 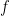 , but such that it is infeasible to sample from the Gaussian distribution without knowledge of the secret basis to instantiate the signature scheme.
, but such that it is infeasible to sample from the Gaussian distribution without knowledge of the secret basis to instantiate the signature scheme.
6: The term syndrome comes from the terminology used for error correcting codes, due to similarities between the 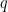 -ary lattices and the error syndrome, which can be used to locate errors in linear codes. Similarly, the matrix
-ary lattices and the error syndrome, which can be used to locate errors in linear codes. Similarly, the matrix 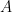 is sometimes called the parity-check matrix for the lattice
is sometimes called the parity-check matrix for the lattice 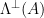 , in analogy to the parity check matrix of linear error correcting codes.
, in analogy to the parity check matrix of linear error correcting codes.
References
[Ajtai96]: M. Ajtai, Generating Hard Instances of Lattice Problems, 1996, https://dl.acm.org/doi/10.1145/237814.237838.
[NR06]: P. Nguyen and O. Regev, Learning a Parallelepiped:Cryptanalysis of GGH and NTRU Signatures, 2006, https://cims.nyu.edu/~regev/papers/gghattack.pdf.
[GPV08]: C. Gentry et al., How to Use a Short Basis:Trapdoors for Hard Lattices and New Cryptographic Constructions https://eprint.iacr.org/2007/432.pdf.
[Falcon]: P. Fouque et al., Falcon: Fast-Fourier Lattice-based Compact Signatures over NTRU, 2020, https://falcon-sign.info/falcon.pdf.
[Dilithium]: S.Bai et al., CRYSTALS-Dilithium Algorithm Specifications and Supporting Documentation (Version 3.1), 2021, https://pq-crystals.org/dilithium/data/dilithium-specification-round3-20210208.pdf.
[BR96]: M. Bellare and P. Rogaway, The Exact Security of Digital Signatures – How to Sign with RSA and Rabin, 1996, https://www.cs.ucdavis.edu/~rogaway/papers/exact.pdf.
[GGH]: O. Goldreich et al., Public-Key Cryptosystems from Lattice Reduction https://www.wisdom.weizmann.ac.il/~oded/PSX/pkcs.pdf.
[Pei10]: C. Peikert: An Efficient and Parallel Gaussian Sampler for Lattices, 2010, https://eprint.iacr.org/2010/088.pdf.
